Creación de un Modelo Digital de Elevación (Procesos de Interpolación) con ARCGIS 10

Por Raúl Martínez

1. Concepto:

Los métodos indirectos para la creación de modelos digitales de elevación incluyen el tratamiento de datos de elevación obtenidos por diversas fuentes. Generalmente los datos obtenidos no son suficientes para cubrir un área de estudio.

La construcción de un MDE entendido como una matriz regular a partir de información vectorial (puntos o líneas), es un problema de interpolación: El planteamiento es el siguiente: dado un conjunto de puntos con coordenadas (x,y,z), distribuidos irregularmente, generar un nuevo conjunto de puntos localizados en los nodos de una red regular de forma que la superficie interpolada sea una representación de la original con una perdida mínima de información.

La interpolación predice valores para las celdas de un ráster a partir de una cantidad limitada de puntos de datos de muestra. Puede utilizarse para prever valores desconocidos de cualquier dato de un punto geográfico, tales como: elevación, precipitaciones, concentraciones químicas, niveles de ruido entre otros.

La suposición que hace que la interpolación sea una opción viable es que los objetos distribuidos espacialmente están correlacionados espacialmente; es decir, las cosas que están cerca tienden a tener características similares. Por ejemplo, si llueve de un lado de la calle, se puede prever con un alto nivel de confianza que está lloviendo del otro lado de la calle. Tendría menos certeza sobre si está lloviendo en todo el pueblo, y menos aún acerca del estado del tiempo en el condado vecino.

Con esta analogía, resulta sencillo ver que los valores de los puntos cercanos a los puntos de muestra tienen más posibilidades de ser similares que los que están más alejados. Esta es la base de la interpolación. Un uso común de la interpolación de punto es crear una superficie de elevación a partir de un conjunto de mediciones de muestra.

Existen variados métodos de interpolación basados en algoritmos matemáticos los cuales pueden ser divididos en:

Métodos Deterministas: Los métodos de interpolación deterministas asignan valores a los lugares sobre la base de los valores medidos y los alrededores especificados en fórmulas matemáticas que determinan la suavidad de la superficie resultante. Los métodos deterministas incluyen:

IDW (ponderación de distancia inversa),
Vecino Natural
Trend
Spline 

Métodos Geoestadísticos: Los métodos geoestadísticos se basan en modelos estadísticos que incluyen autocorrelación (la relación estadística entre los puntos medidos). Debido a esto, técnicas geoestadísticas no sólo tienen la capacidad de producir una superficie de predicción, sino también proporcionar un cierto grado de certeza o la exactitud de las predicciones.

· Kriging

2. Generación de MDE

En este laboratorio, aplicaremos los diferentes métodos de interpolación presentes en el programa ArcGis. V10 tomando como insumo curvas de nivel y cotas de elevación del sector del valle de Antón y El monumento Natural de Barro Colorado respectivamente.

2.1 Encienda su Arcgis

Llamar la cobertura elevación50.shp y polígono_corte50 localizada en la carpeta interpolación\valle_anton. Estas coberturas muestran valores de elevación a nivel de puntos y los límites del área señalada.

Los diferentes métodos de interpolación que posee ArcGis, se encuentra localizados en el ambiente Spatial Analyst Tools de ArcTool Box. Arcgis posee 6 métodos de interpolación definidos:

IDW, Kriging, Natura Neigbor, Spline, Trend y TopoRaster.

  

 

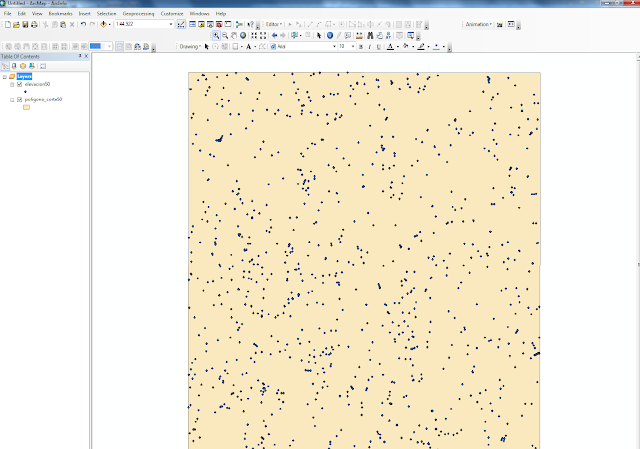
Despliegue de las cobertura de puntos de elevación del sector del valle de Antón. 

 

Desarrollo de los métodos de Interpolación:

1.      IDW (Ponderación de Distancia Inversa):

Este método de interpolación asume que cada punto posee una influencia local que disminuye con la distancia. De esta manera, el método pondera con mayor fuerza a los puntos cercanos a la celda proceso y con menor intensidad sobre aquellos ubicados a mayor distancia. Para definir el valor de cada celda, el programa puede realizar una búsqueda en base a una serie definida de puntos o puede buscar a todos aquellos puntos que se encuentren al interior de un radio de búsqueda determinado.

Este método es apropiado cuando la variable analizada disminuye conforme aumenta la distancia desde cada punto analizado. Por ejemplo cuando se intenta interpolar una superficie que representa el poder adquisitivo de los consumidores respecto de una tienda. Mientras más lejos se encuentren los consumidores de la tienda, menor será la influencia ejercida por las entidades para atraer a los potenciales clientes y viceversa.

IDW estima los valores de las celdas promediando los datos obtenidos desde los puntos de entrada ingresados que están más cercanos a ella. Sin embargo existen algunos parámetros que pueden ser configurados para modificar o ajustar los resultados entregados

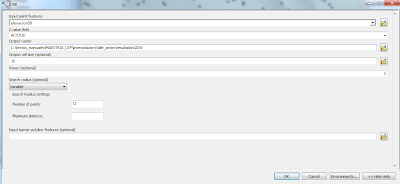
Power (potencia): Mediante IDW es posible controlar - basándose en la distancia - la importancia de los puntos conocidos sobre los valores interpolados. Al definir una potencia alta, mayor será el énfasis sobre los puntos más cercanos y el resultado de la superficie será más detallado (pero menos suavizado). Especificando una potencia menor, se le dará una mayor importancia a los puntos más distantes y por tanto la superficie resultante será más suave.

Las características de la superficie interpolada pueden ser controladas también al limitar el número de puntos utilizados en los cálculos.

Radius Type: Fixed Utilizando un radio de búsqueda definido (Fixed), para cada punto interpolado, todos los puntos que se encuentren al interior del radio de búsqueda (circular o también definido como isotrópico) serán utilizados. Especificando un mínimo de puntos en la búsqueda asegura que de no encontrarse puntos dentro del radio, este aumentará hasta encontrar la cantidad de puntos definida con anterioridad por el usuario.

Radius Type: Variable Utilizando un radio de búsqueda variable, el número de puntos utilizados en la interpolación es fijo y por lo tanto el radio de búsqueda variara dependiendo de cuán lejos se encuentren los puntos definidos con anterioridad. Esta modalidad de búsqueda puede producir mejores resultados cuando la densidad de los puntos varía de una zona a otra. Si se tienen áreas con pocos datos quizá sea necesario restringir el área de búsqueda aunque disminuya el número de puntos participes de la interpolación.

Barrier: Una línea o polígono puede ser utilizado como barrera o quiebre que limita la búsqueda de puntos. Una línea puede representar un risco, acantilado o cualquier otra interrupción sobre el paisaje. Solo aquellos puntos ubicados en el mismo lado de la celda proceso serán utilizados.

Aplicando el proceso tenemos:

 Resultado

Ejecute nuevamente el proceso ahora con una potencia de 3 y 0.5 respectivamente. Compare

1.      Natural Neighbor (Vecino Natural)

Al igual que IDW, este tipo de interpolación utiliza un método de ponderación promediada. Sin embargo, en vez de generar un valor de interpolación basado en el promedio ponderado de sus distancias, la interpolación de tipo Natural Neighbor (“cercanía” o “proximidad natural”) genera una triangulación de Delauney a partir de las locaciones medidas y selecciona los nodos más cercanos para crear polígonos o escudos convexos alrededor de las locaciones que los conforman. Luego, pondera sus valores en base a un área proporcionada.

  

  

Este método es el más adecuado cuando los valores se encuentran distribuidos de manera desigual. Es una técnica de interpolación muy adecuada para propósitos genéricos.

Resultado

 

3. Spline (Curvatura mínima)

Este método de interpolación de uso genérico ajusta una superficie de curvatura mínima a través de los puntos ingresados. Es adecuado para mostrar variaciones graduales de superficies como por ejemplo elevaciones o concentraciones de polución. Sin embargo puede no ser útil cuando existen una gran cantidad de variaciones en una distancia horizontal relativamente pequeña.

Este método es indicado para valores que varían muy poco y lentamente. No obstante es un método de interpolación inexacto, ya que altera ligeramente el valor y la posición de los datos originales, generando un resultado muy suavizado. Este método es recomendable para cuando tenemos poco puntos de partida, ya que posibilita obtener nuevos datos.  Cuando los cambios son muy abruptos no se recomienda utilizar este interpolador.

Hay dos métodos Spline:

Regularized: El método Regularizado crea una superficie suave, de manera gradual cambiando la superficie con los valores que pueden estar fuera de la gama de datos de la muestra.

Tension: El método de Tensión suaviza la rigidez de la superficie según el carácter del fenómeno modelado. Esto crea la superficie lisa con valores estrechamente obligados por la gama de datos de la muestra.

La formula también permite otras opciones.

Weight: Define el peso de la tercera derivada de la superficie en la expresión de minimización de curvatura. Más alto el peso, más lisa la superficie.

Los valores típicos que pueden ser usados son 0; 0.001; 0.01; 0.1, y 0.5.

Aplicando Sline en ArcGis:

Resultado

4.      Trend (Tendencia)

Este método de interpolación ajusta una función matemática (Polinomial de un orden especificado por el usuario) a todos los puntos ingresados. Trend utiliza un ajuste de regresión del menor cuadrado que da como resultado un Raster que minimiza la varianza de la superficie en relación a los puntos ingresados. Esta superficie está construida de manera tal que para cada locación de interpolación, el total de las diferencias entre los valores actuales y los valores estimados (la varianza) será siempre lo más pequeño posible. De esta manera el resultado final será un Raster que contiene la tendencia generalizada de los valores contenidos en los puntos ingresados.

Aplicando Trend en ArcGis:

Resultado

 

5.         Kriging

Un segundo grupo de métodos de interpolación consiste en los métodos geoestadísticos (Geostatistical Methods) como es el caso de Kriging. Los cuales están basados en modelos estadísticos que incluyen por ejemplo la autocorrelación (relación estadística entre los valores medidos). Debido a esto, no sólo estas técnicas poseen la capacidad de producir una superficie de predicción, sino que además, proveen algunas herramientas para medir la certeza o precisión de estas predicciones.

El método de interpolación Kriging asume que la distancia y/o la dirección entre puntos de muestreo es una expresión de la correlación espacial entre los puntos y que por tanto dicha información puede utilizarse para explicar la variabilidad encontrada en la superficie muestreada. El algoritmo ajusta una función matemática a un determinado número de puntos o a aquellos que se encuentren en un radio de búsqueda.

En IDW, la ponderación depende solamente de la distancia hacia la locación a predecir. Sin embargo, en el Kriging, las ponderaciones están basadas no solo en la distancia entre las locaciones medidas y la predicción realizada sino que además se considera la forma en cómo se organiza espacialmente la totalidad de los puntos localizados sobre una superficie.

Para utilizar la organización de los datos en la ponderación, es necesario cuantificar la correlación espacial de las mismas. De esta manera, en el Ordinary Kriging, la ponderación depende del modelo de ajuste de los datos medidos, la distancia hacia las locaciones de predicción y la relación espacial entre valores medidos alrededor de las locaciones de predicción.

Este interpolador es más complejo que los anteriores y normalmente requiere de cierto conocimiento estadístico por parte del usuario(a). El análisis incluye los siguientes pasos:

·         análisis estadístico exploratorio del set de datos

·         modelado del variograma

·         interpolación de la superficie

·         análisis de la superficie de varianza.

Aplicando Kriging en ArcGis:

 Resultado

 

4.      TOPO Raster:

Utiliza una técnica de interpolación diseñada específicamente para crear una superficie que representa con mayor precisión una superficie de drenaje natural y preserva mejor los cordones montañosos y las redes de transmisión de los datos de curvas de nivel de entrada.

Esta herramienta permite imponer restricciones en el proceso de interpolación como lagos, red de drenaje, condiciones de frontera y sumideros con el fin de que resulte una estructura correcta en la representación de crestas y arroyos.

El algoritmo que se utiliza está basado en el de ANUDEM, desarrollado por Hutchinson y otros en la Universidad Nacional de Australia y presentado por ESRI como una opción para generara DTM hidrológicamente correctos.

Los parámetros que requiere esta función se describen a continuación.

Input feature Data: Permite introducir los archivos que vamos a utilizar para realizar la interpolación. Podemos indicar seis tipos diferentes de datos: contornos (CONTOUR), puntos (POINTELEVATION), drenajes (STREAM), sumideros (SINK), condición de frontera (BOUNDARY) y/o lago (LAKE).

El algoritmo recibe todo los tipos de datos simultáneamente; por ejemplo si quisiéramos realizar una interpolación a partir de unos puntos pero queremos que delimiten los lagos y además existe un límite donde la altura es cero, debemos introducir al sistema los respectivos archivos que contenga los puntos con las alturas (POINTELEVATION), el shape de lagos (LAKE) y el shape con la condición de frontera (CONTOUR). Veamos uno a uno estos parámetros. 
POINTELEVATION: Feature que contiene las elevaciones de la superficie. El archivo deberá contener campos con datos XYZ.
CONTOUR: Feature de línea que representa las curvas de nivel del terreno. El archivo debe contener un campo que contenga las alturas de las curvas de nivel.
STREAM: Feature contiene la red de drenaje.
SINK: Feature que contiene o representa las depresiones topográficas del terreno. El archivo debe incluir un campo con las elevaciones de los sumideros.
BOUNDARY: Feture de línea o poligono que permite especificar condiciones de frontera para la realización de la interpolación. Por ejemplo podemos indicar donde termina un lago, donde la altura o el espesor es cero, en fin….
LAKE: Un Feature que permite especificar la localización de lagos.
Output surface raster: Indicamos la ruta y el nombre del archivo de salida.
Output cell size: Tamaño de las celdas del archivo de salida.
Output extent (optional): Permite especificar un archivo o las coordenadas de los límites de la interpolación.

Estas funciones son las básicas para la optención de la superficie calculada

Para el desarrollo del Topogrid, utilice las siguientes coberturas:

· Curvas50 (curvas de nivel del mapa 1:50,000)
· drenaje_50 (red de drenaje)
· polígono_corte (límite del área de estudio)
· cota50 (cotas de elevación de cerros)
· elevación50 (cotas de elevación)

 Resultado

 

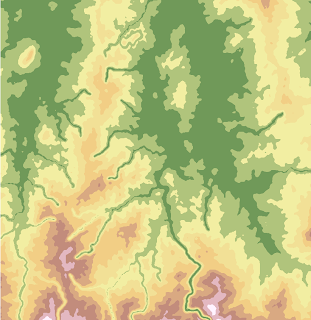
6.         TIN (Red de triángulos irregulares)

Las TIN son una forma de datos geográficos digitales basados en vectores y se construyen mediante la triangulación de un conjunto de vértices (puntos). Los vértices están conectados con una serie de aristas para formar una red de triángulos. Existen diversos métodos de interpolación para formar estos triángulos, como la triangulación de Delaunay o el orden de distancias. ArcGIS es compatible con el método de triangulación de Delaunay.

La triangulación resultante cumple el criterio de triángulo de Delaunay, que afirma que la circunferencia circunscrita de cada triángulo de la red no debe contener ningún vértice de otro triángulo. Si se cumple el criterio de Delaunay en todo el TIN, se maximizará el ángulo interior mínimo de todos los triángulos. El resultado es que los triángulos finos y largos se evitan en lo posible.

Las aristas de los TIN forman facetas triangulares contiguas y no superpuestas que se pueden utilizar para capturar la posición de entidades lineales que juegan un papel importante en una superficie, como cadenas montañosas o arroyos. A continuación encontrará unos gráficos en los que se pueden ver los nodos y aristas de un TIN (izquierda) y los nodos, bordes y caras de un TIN (derecha)

Puesto que los nodos se pueden colocar irregularmente sobre una superficie, las TIN pueden tener una resolución más alta en las áreas donde la superficie es muy variable o cuando se desea obtener un nivel de detalle superior y una resolución más baja en zonas menos variables.

Las TIN se suelen utilizar para el modelado de alta precisión de áreas más pequeñas, como en aplicaciones de ingeniería, donde resultan útiles porque permiten realizar cálculos de área planimétrica, área de superficie y volumen.

Puesto que los nodos se pueden colocar irregularmente sobre una superficie, las TIN pueden tener una resolución más alta en las áreas donde la superficie es muy variable o cuando se desea obtener un nivel de detalle superior y una resolución más baja en zonas menos variables.

Construyendo un TIN en ArcGis:

En la construcción de un TIN, es posible utilizar, al igual que en el TopoRaster, diversas entradas  como cotas de elevación, curvas de nivel, drenaje y polígonos de corte, pudiendo definir en la mayoría de ellos la manera como se incorporan al proceso de interpolación.

Resultado

Fuentes:

http://help.arcgis.com/es/arcgisdesktop/10.0/help/index.html#//009z000000z4000000

http://www.um.es/geograf/sigmur/sigpdf/temario_6.pdf

http://www.etsimo.uniovi.es

Martínez-Casasnovas, J.A., 1999. Modelos digitales de terreno: Estructuras,de datos y aplicaciones en el análisis de formas del terreno y en Edafología.QUADERNS DMACS Núm. 25, Departament de Medi Ambient i Ciències del Sòl, Universitat de Lleida, Lleida.